FIX Error Code 9C59: Internet Explorer Installation failed (IE10, IE11)
Error Code 9C59 may appear when you try to install Internet Explorer 11 (or IE10) via Windows Update. When this problem happens, the Windows Update fails with the following error message: "Some Updates were not installed – Error(s) found: Code 9C59 – Windows Update encountered an unknown error".
The error Code 9C59 in Internet Explorer installation, can occur for several reasons e.g. due to a Windows Update folder (SoftwareDistribution) corruption, Windows Update elements corruption, missing important updates that are needed to install Internet Explorer, etc.
This troubleshooting guide contains detailed instructions on how to resolve the Code 9C59 received during Windows Update.
How to fix Error 9C59 – Internet Explorer installation failed.
- Solution 1: Install all optional Windows Updates & update essential device drivers.
- Solution 2. Delete the SoftwareDistribution folder (Windows Updates Store Folder)
- Solution 3: Use Internet Explorer offline installer.
- Solution 4. Fix Windows Corruption error using System Update Readiness tool (DISM)
- Other solutions to bypass Error 9C59
Solution 1: Install all optional Windows Updates & update essential device drivers
Step 1. Install all Important and Optional updates except Internet Explorer 11.
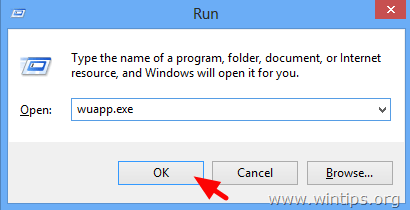
1. Press Windows + R keys to load the Run dialog box.
2. Type the following command to open Windows Update and press Enter.
- wuapp.exe
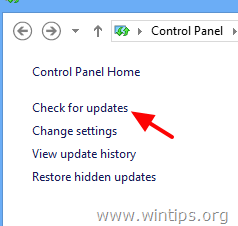
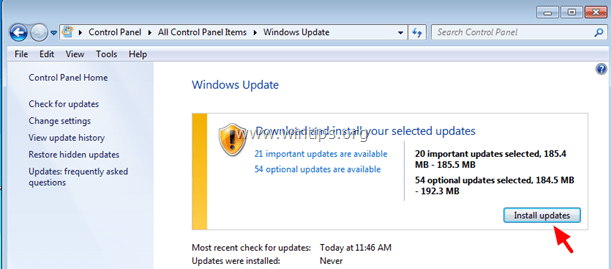
3. Press Check for updates.
4. Choose the Important Updates link.
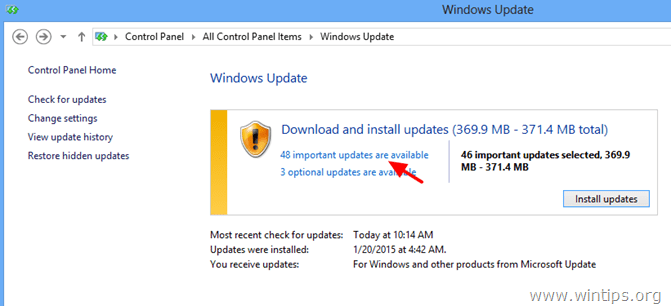
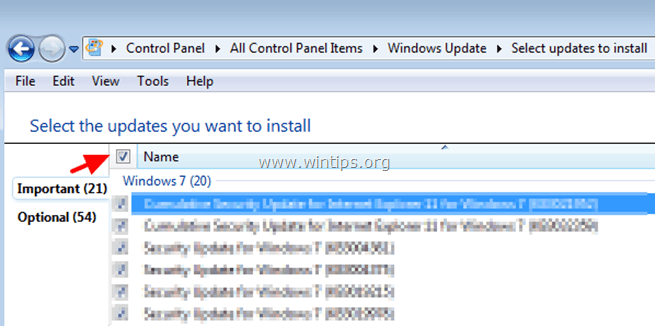
5. First Uncheck and re-check the Name checkbox to select all Important Updates.
5. Then Uncheck the Microsoft Internet Explorer 11 update.
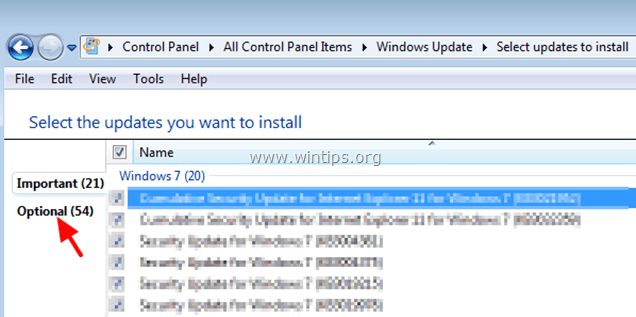
6. Click Optional at the left.
7. Uncheck and re-check the Name checkbox to select all Optional Updates and click OK.
8. Finally choose to Install Updates.
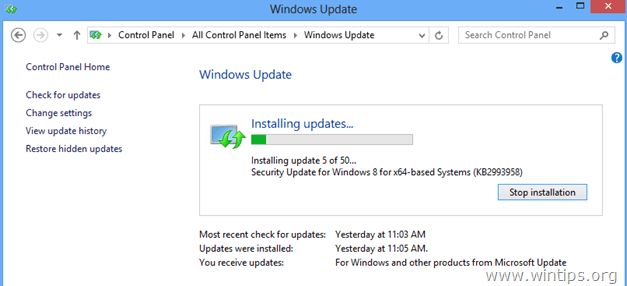
—– Be patient while Windows install updates —–
9. After Windows Updates are installed, perform the same procedure until you install all available updates EXCEPT IE11.
Step 2. Update essential device drivers.
1. Download and Install from the manufacturer's website the latest drivers for the following devices:
- Display Adapter
- Wireless Adapter
- Ethernet Adapter
Step 3. Install Internet Explorer 11
1. When you perform the above steps try to install Internet Explorer again. If you still face problems, try solution 2 below.
Solution 2. Delete the SoftwareDistribution folder (Windows Updates Store Folder)
The SoftwareDistribution folder, is the location where Windows stores the downloaded updates. If this folder is corrupted, then you will face problems during Windows Update. So, another solution to bypass the error 9C59 during Windows Update, is to delete (or rename) that folder* and restart your computer. To delete the SoftwareDistribution folder:
* Note: Upon restart, the next time the Windows Update checks for available updates, a new empty SoftwareDistribution folder will be create automatically to store updates.
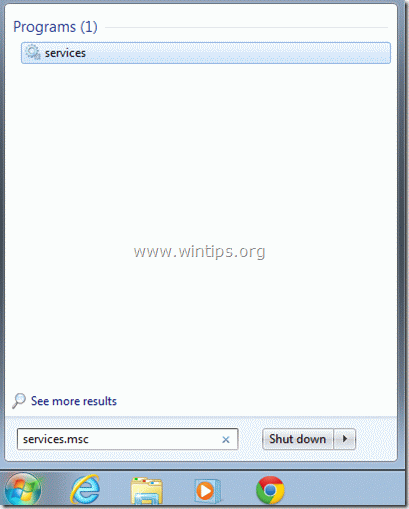
1. Simultaneously press Windows key + R to open run command box.
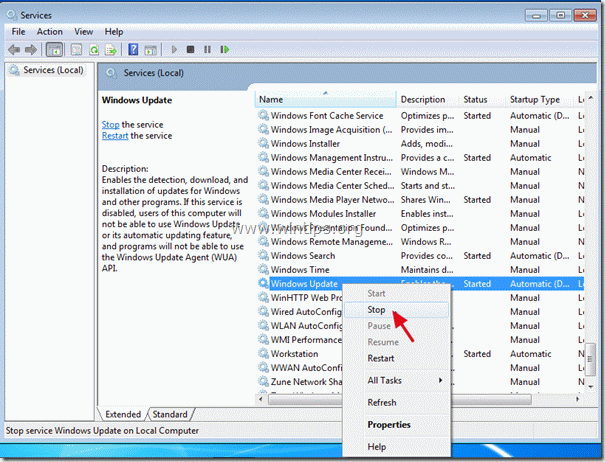
2. In run command box, type: services.msc and press Enter.
3. Search for Windows Update service, then right click on it and select Stop.
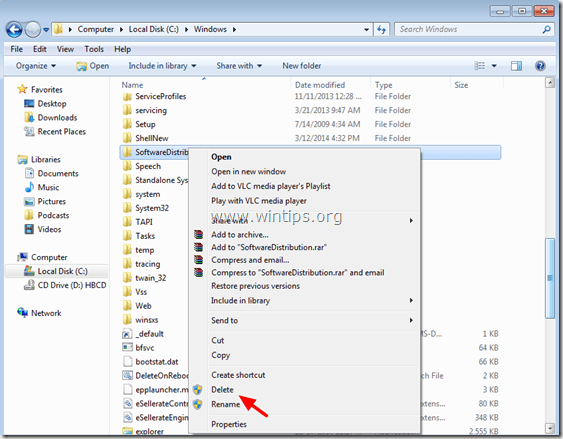
3. Navigate to “C:Windows”folder.
4. Delete (or Rename e.g. to “SoftwareDistributionOLD”) the “SoftwareDistribution” folder.
5. Restart your computer and then try to install Internet Explorer.
Solution 3: Use Internet Explorer 11 offline installer.
Step 1: Uninstall previous version of Internet Explorer from Control Panel
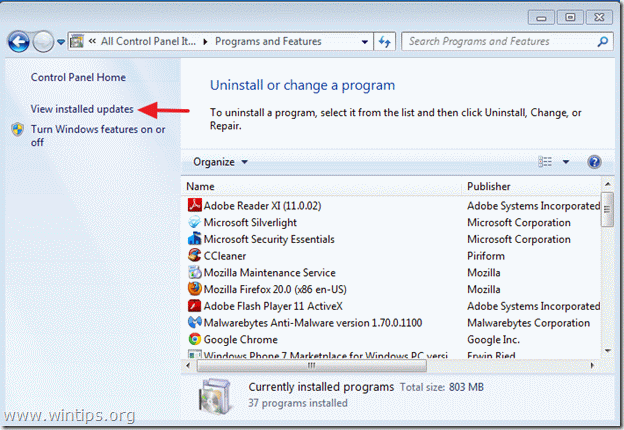
Navigate to Windows Control Panel & open Programs & Features > View Installed Updates and uninstall any previous version of Internet Explorer.
1. Press “Windows” ![]() + “R” keys to load the Run dialog box.
+ “R” keys to load the Run dialog box.
2. Type “appwiz.cpl” and press Enter.
3. In the “Programs and Features” window, click on “View installed updates” on the left pane.
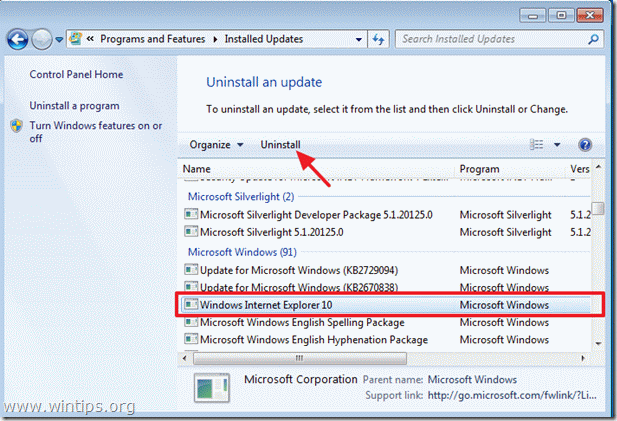
4. From the list of installed programs, locate Internet Explorer and click “Uninstall”.
5. When uninstallation is completed, restart your computer for changes to take effect and revert back to Internet Explorer 9.
Additional Help:
- If your computer doesn't revert to IE 9 automatically, then you can download and install Internet Explorer 9 manually.
Download Internet Explorer 9 for Windows 7 (32-bit)
Download Internet Explorer 9 for Windows 7 (64-bit)
Download Internet Explorer 9 for Windows Vista (32-bit)
Download Internet Explorer 9 for Windows Vista (64-bit)
Step 2: Download Internet Explorer Offline Installer.
Use an Internet Explorer 11 Offline installer package to install IE11.
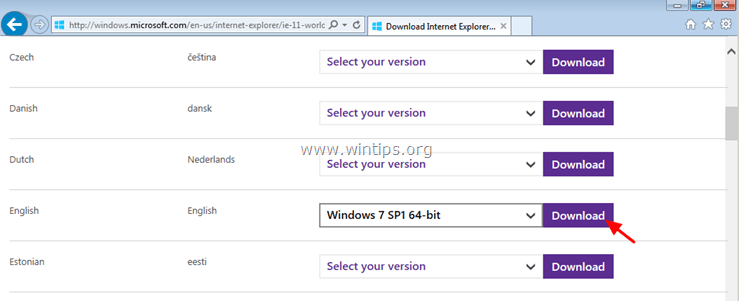
1. Navigate to Microsoft's IE download site and download Internet Explorer 11 Offline Installer according to your system language and Windows 7 version:
2. When the download is completed, double-click at the downloaded file (e.g. "IE11-Windows6.1-x64-en-us.exe") to install IE11.
3. When the installation is completed, restart your computer.
Solution 4. Fix Windows Corruption error using System Update Readiness tool (DISM)
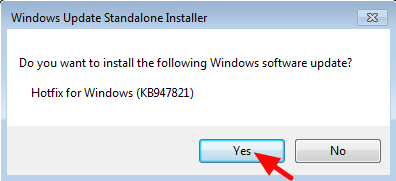
1. Download and save to your desktop the System Update Readiness tool according to your Windows version.
2. Double click to install the downloaded file (e.g. Windows6.1-KB947821-v34-x86.msu).
3. When the installation is completed, restart your computer and try to install Internet Explorer again.
Other solutions to try if the above solutions don't work:
1. Reset Windows Updates Components by running the FixIt tool from this link.
2. Make sure that you have installed the following prerequisite updates for Internet Explorer:
3. Free up disk space by running Disk Cleanup.
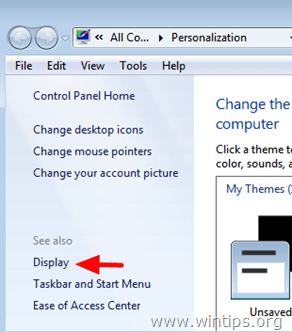
3. Change DPI to default settings.
1. Right-click on an empty space on your desktop and click Personalize.
2. Click Display at the left.
3. Select the Smaller – 100% (default)
Good luck!
We're hiring
We're looking for part-time or full-time technical writers to join our team! It's about a remote position that qualified tech writers from anywhere in the world can apply. Click here for more details.
- How to Disable or Remove BitLocker from Windows RE. - April 24, 2024
- FIX: Error 0x8007025d in Windows 10 Update. - April 22, 2024
- How to Disable Device Encryption in Windows 11/10. - April 17, 2024







February 20, 2019 @ 8:28 pm
Performed every step in the article, then got down to the comments section. Ran Disk Cleanup on Drive C: as recommended, for both temporary and system files. Deleted Gb's of files. Was able then to install IE11.
February 4, 2017 @ 11:58 am
Tried most of the things here, no joy. Finally restored Win7 to fix the prob.
Thing is that we were not able to install IE11 for ages, the record showed fail after fail going back since it's release. I never cared since we used Chrome. In fact, it wasn't until we tried to load the new QuickBooks that the failure to load IE became apparent.
A pain but all over now. Why can't MS figure something like this out? Too busy helping out NSA?
June 29, 2016 @ 4:32 pm
Thanks Colleen, worked a treat when everything else failed.
I had to carry out a full disk clean up as a partial clean didn't work.
July 5, 2016 @ 3:26 am
You are very welcome! Very happy it worked for you too John K!
May 8, 2016 @ 8:29 pm
You are the man!!! Thanks Colleen
July 5, 2016 @ 3:23 am
No I'm the woman! :) You are very welcome Hans!
April 19, 2016 @ 11:33 pm
After trying all of the above on this site. And spending days upon days trying to find a solution on other sites. I finally came across an easy fix someone posted…. and it worked!!!! Do a disk cleanup on drive C: and then install IE 11. Rebooted and now I have IE 11 as my browser. :)
April 27, 2016 @ 1:32 am
Colleen I am in love with you. Like you I tried everything above and lots more over the last two weeks and your simple solution worked. Why on earth don't Microsoft know this? Thank you so much. Dave x
July 5, 2016 @ 3:17 am
I just came back across this! Thanks for the nice compliments, I'm glad it worked for you too! Microsoft is dumb lol You are very welcome! Colleen
May 3, 2016 @ 12:56 pm
I just want to say, COLLEEN CHAPMAN.. THANK YOU.
I went through all of these, all of the Microsoft garbage articles with waste of time 'solutions', and obviously, you can tell by my frustration, I just wasted hours upon hours.
Until…I came to Colleen's post here. Whew. I was this close to telling the client we'll need to reload his computer because IE is such a cludge.
Thank you again Colleen for sharing and being a hero.
July 5, 2016 @ 3:22 am
You are very welcome Phil! No hero, just one determined girl to get it fixed! It was aggravating the heck out of me. Glad you didn't have to reload your clients computer. :)
May 3, 2017 @ 2:14 pm
Love you… Super Happy! I tried everything that Microsoft and other sites asked me to do, but this simple thing worked like a charm. Thanks Colleen
April 4, 2016 @ 3:54 am
Windows 7 IE-11 9C59 Error. If you've tried everything else and are at your wits end, try this (at your own risk of course!).
Go to Control Panel / Programs & Features / View Installed Updates / Turn Windows features on or off. Check if IE says 11 and is checked on. This was my situation. It appears that part of it was installed and getting in the way of subsequent attempts. We have to remove all that.
1. Download manual IE-11 install: http://windows.microsoft.com/en-us/internet-explorer/ie-11-worldwide-languages
2. Open a Command Prompt as Administrator. Find Icon / hold shift key / right click mouse / Run As Administrator. Put that aside for a moment.
3. Find IE-11 packages that it thinks it has installed and uninstall them manually. Open a Windows Explorer and navigate to: c:\windows\servicing\packages.
A. Find all references to IE-11. There will be several of them (~~ 11.X.X with .mum and .cat)
Example: Microsoft-Windows-IE-Hyphenation-Parent-Package-English~31bf3856ad364e35~~~11.2.9412.0
B. Left click the filename once, wait then left click again (highlighted except extension), Ctrl-c to copy.
C. Now go to Command Prompt window and type: pkgmgr /up: (then right click paste)
Example: pkgmgr /up:Microsoft-Windows-IE-Hyphenation-Parent-Package-English~31bf3856ad364e35~~~11.2.9412.0
D. IMPORTANT: After you hit enter, go back to the Windows Explorer and wait until the package disappears by rereading the directory (F5). Keep waiting / F5 until it is gone.
E. Do the rest of the IE-11 entries in that directory until they are all gone.
4. Install the IE 11 that you downloaded from step 1. It will ask you to reboot at the end.
Hopefully you will have IE 11 at that point!!
February 19, 2016 @ 5:25 pm
Link for DotNet 4.61
http://filehippo.com/download_dotnet_framework_4/
January 31, 2016 @ 3:14 am
I found the easiest way to resolve the issue purely by accident. By mistake I removed
Net Framework 4.5 and found IE 10 and 11 both installed without a problem. I then
installed Net Framework 4.61 restarted the computer. I now have IE 11 and everything
works fine.
January 31, 2016 @ 11:42 pm
Hi John,
I get the message "We are sorry, the page you requested cannot be found. " from the microsoft download site for .net 4.6.1
Where did you download it from?
January 15, 2016 @ 11:38 pm
To the person(s) who wrote this article: Thank you, thank you, thank you! I've been beating my brains out for days trying to get IE 11 installed on my wife's PC, and none of the numerous other articles I read did the trick. At one point last night I was getting so frustrated that I considered the possibility of sacrificing a goat to the Windows gods! Here's what finally worked: renaming the SoftwareDistribution folder. After that, the offline installer ran successfully (which it never did before), so now I don't have to explain to my wife why she has to choose between IE 8 (one of the previous attempts involved removing IE 9, and trying to reinstall it didn't work, either) and Firefox or Chrome. Again, thank you!
January 4, 2016 @ 3:34 am
Oh boy….There has NEVER in the past been a big problem updating IE….WHY IS THERE ONE NOW?
I simply DO NOT understand how, if Microsoft can figure out how to quietly install Windows 10 piece by piece and have a sub-program running and hogging the better part of 1gb of my ram and up to 100% of my CPU, that they cannot – probably COULD NOT – make an installer for IE11 that can, in one shot, scan my computer, install the needed updates and then install IE 11 with one command!
I found out the easy way that installing google chrome had NONE of these problems!
Now – as for whether I trust Google more than Microsoft or not, in their data mining endeavours, is a whole separate issue…
thanx
January 15, 2016 @ 11:45 pm
David, at the risk of sounding like the old cynic that I am, I suspect we both have a pretty good idea why the Microsofties aren't making any noticeable effort to produce a bulletproof IE 11 installer for Win 7: They want all of us holdouts to stop resisting their effort to move everyone to Win 10 (shades of Star Trek: "'Resistance is futile. You will be assimilated").
December 3, 2015 @ 12:50 am
Thomas's comment is what worked for me and i tried ALOT of other things first. The command he has listed is missing a couple slashes but here is the correct one.
FORFILES /P %WINDIR%\servicing\Packages /M Microsoft-Windows-InternetExplorer-*11.*.mum /c “cmd /c echo Uninstalling package @fname && start /w pkgmgr /up:@fname /norestart”
December 11, 2015 @ 6:21 pm
The syntax in Matt Dyar's post is correct, but you may get an error about /c only being allowed once if you copy/paste from your web browser. If that happens, delete the quotes from the command and retype them to change them from "smart" quotes to regular quotes. I guess smart is not always smarter :)
September 23, 2015 @ 9:51 am
I used Thomas' instructions on the elevated command after following all the others above and it worked for me.
I'm not sure why the elevated command didn't work initially. I compared it to the pasted version below and it looks the same. You may have to follow the Wiki on his example to get the original, but after I used it and restarted windows, it automatically installed IE11. I didn't even have to follow the directions after that, though I had tried several other times to manually install on the other link he provided prior to that and it had not worked, so maybe it the IE11 install was cached somewhere.
(from http://www.wikihow.com/Uninstall-Internet-Explorer-11-for-Windows-7 )
FORFILES /P %WINDIR%\servicing\Packages /M Microsoft-Windows-InternetExplorer-*11.*.mum /c "cmd /c echo Uninstalling package @fname && start /w pkgmgr /up:@fname /norestart"
August 5, 2015 @ 3:57 am
This is how I was able to get IE11 to install:
Uninstall IE10 restart
Uninstall IE9 restart
Run the following command at an elevated command prompt:
FORFILES /P %WINDIR%servicingPackages /M Microsoft-Windows-InternetExplorer-*11.*.mum /c "cmd /c echo Uninstalling package @fname && start /w pkgmgr /up:@fname /norestart"
(from http://www.wikihow.com/Uninstall-Internet-Explorer-11-for-Windows-7 )
Restart
Go to:
Start_Control Panel_Programs_Programs and Features_Turn Windows Features On or Off.
You should see a list of programs with check boxes to their left. Make sure you see Internet Explorer 8 listed. If you see Internet Explorer 8 listed you should be able to install the Internet Explorer Standalone Update found here:
http://windows.microsoft.com/en-us/internet-explorer/ie-11-worldwide-languages
March 18, 2016 @ 9:25 pm
When I tried to run your code at the command prompt I get an error message "The specified directory does not exist" any ideas?
March 19, 2016 @ 9:41 am
@Dennis: Use this command instead: FORFILES /P %WINDIR%\servicing\Packages /M Microsoft-Windows-InternetExplorer-*11.*.mum /c "cmd /c echo Uninstalling package @fname && start /w pkgmgr /up:@fname /norestart"
March 31, 2016 @ 11:43 am
lakonst your Awesome Man its working for me .. Thank U so much
May 21, 2016 @ 3:47 pm
I have tried this a number of times but I keep getting "Access Denied"
I have unlocked everything with WinOwnership as well as setting permissions to my admin user
I cannot get any windows updates to work
May 22, 2016 @ 12:40 pm
@Kevin Whitcomb: In which step (solution) you receive the "Access Denied" message?